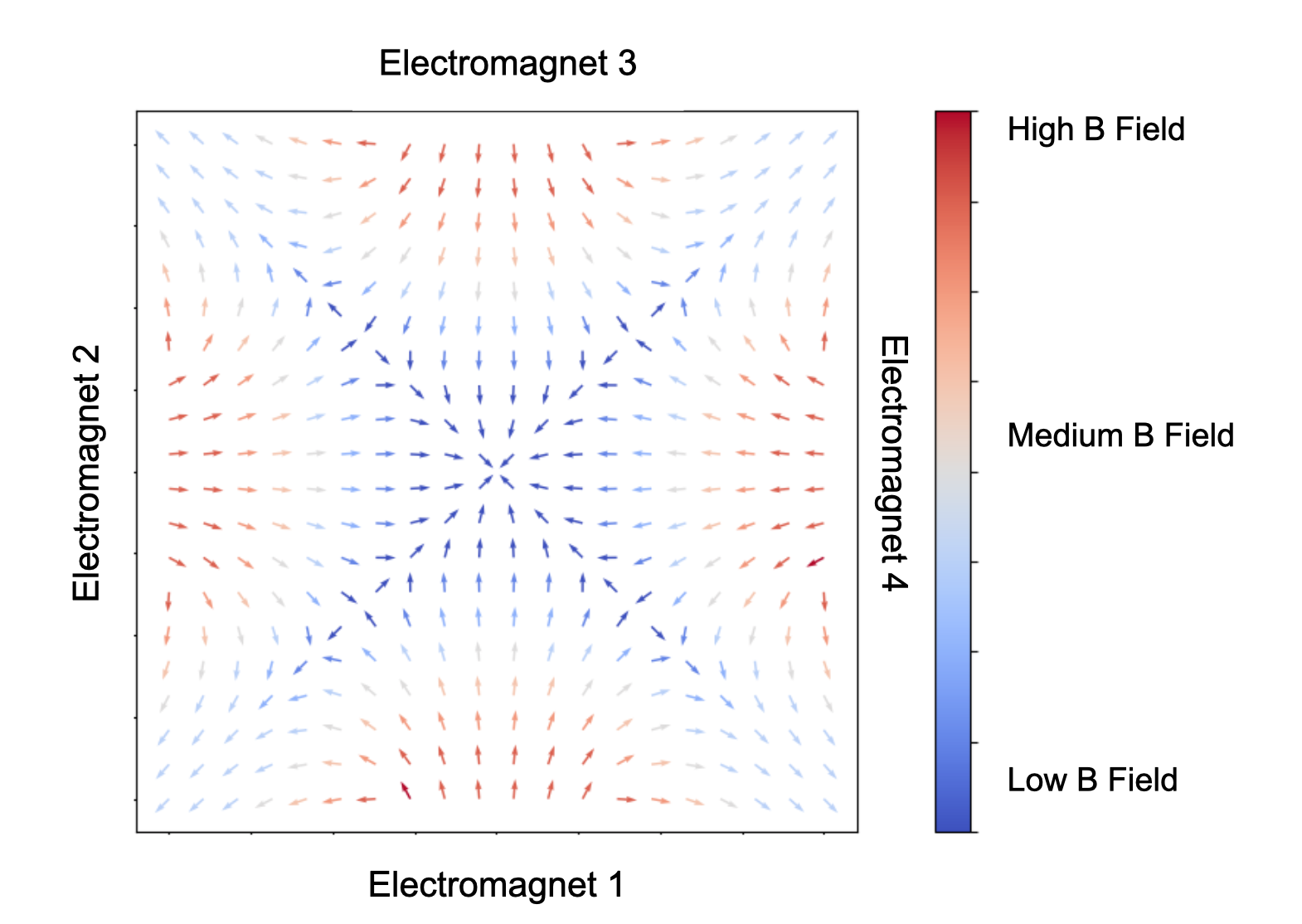
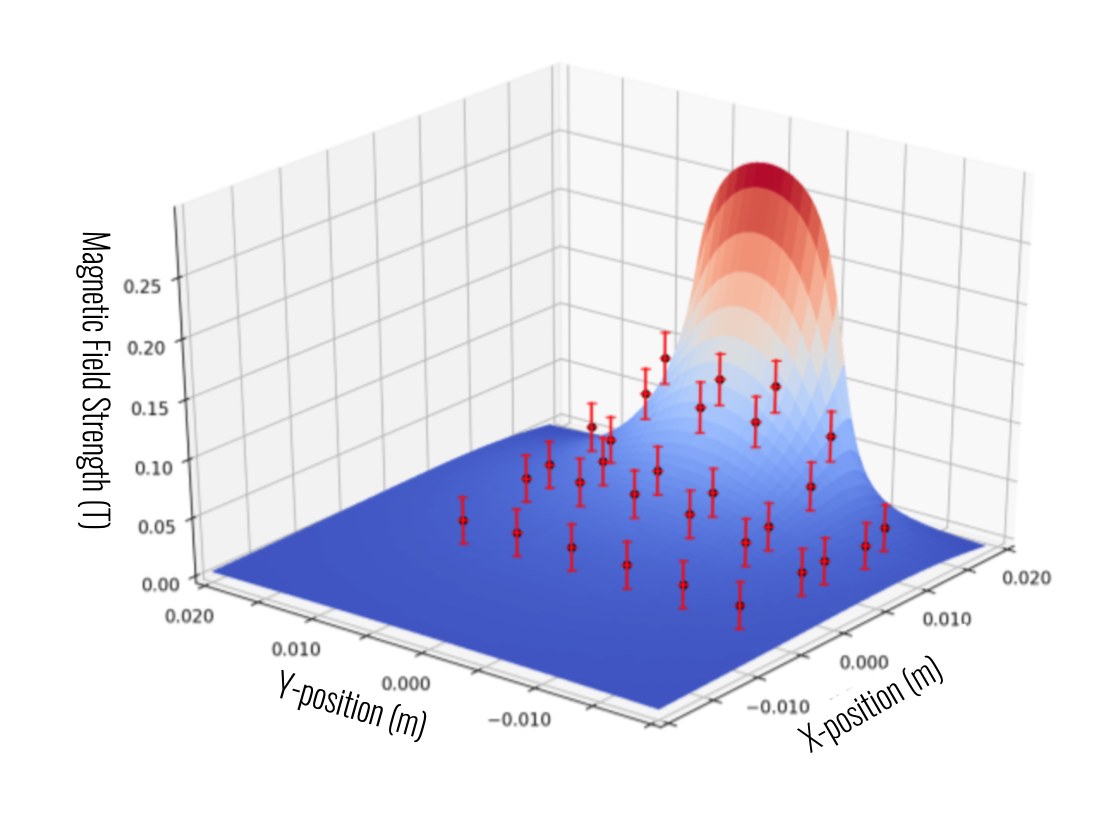
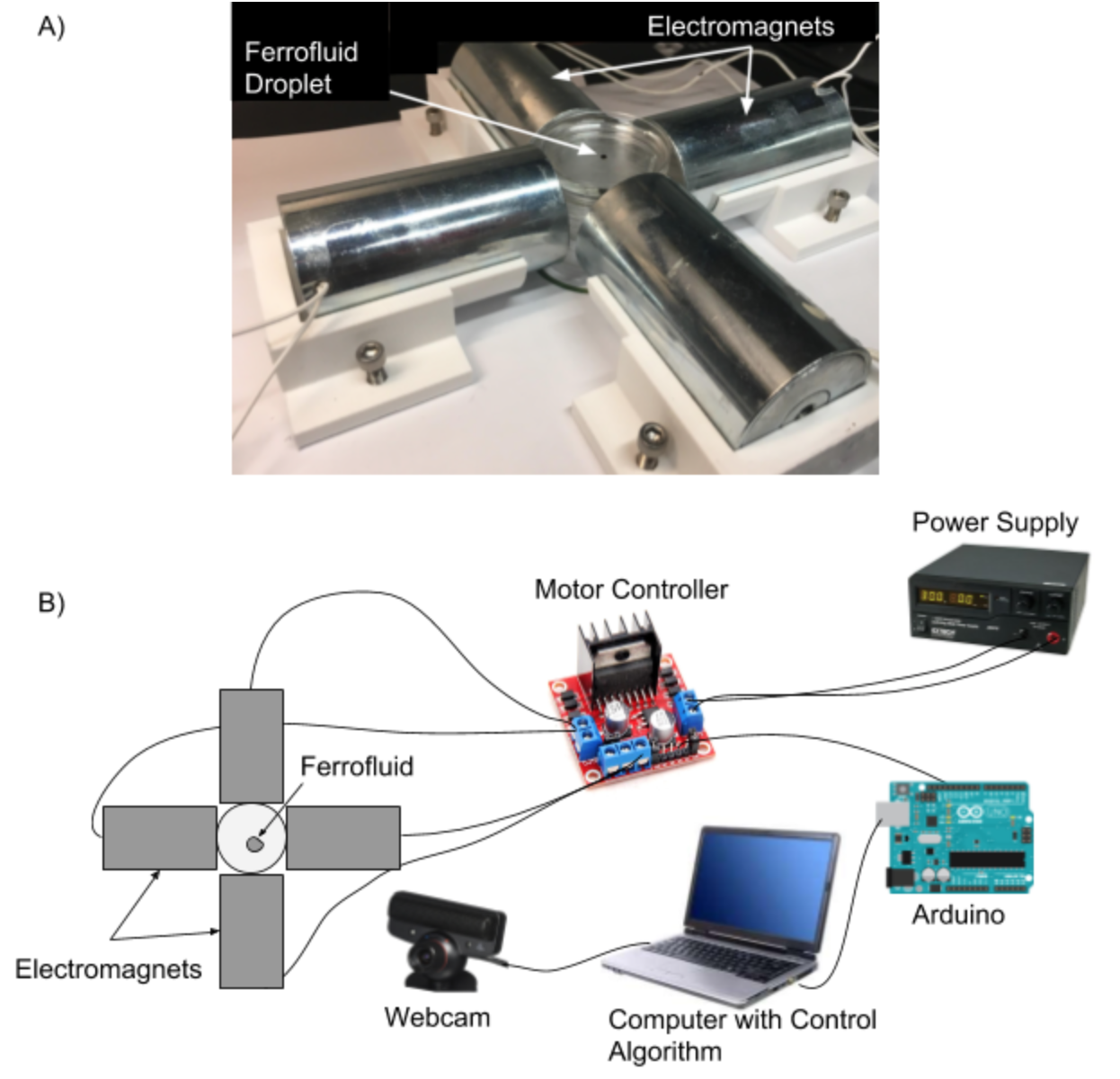
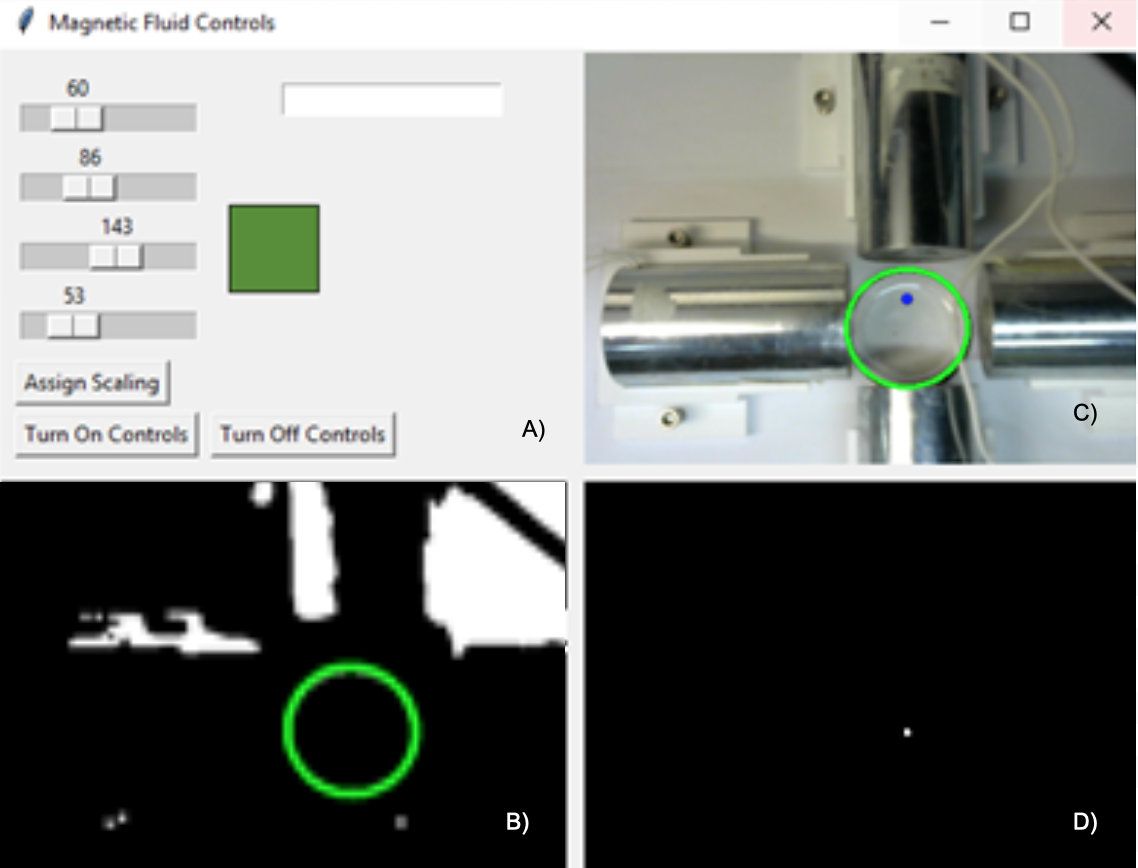
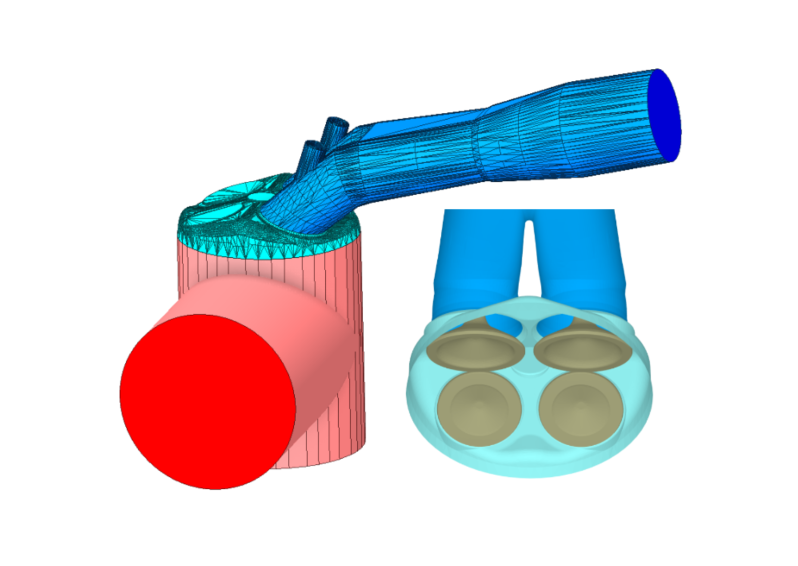
Background
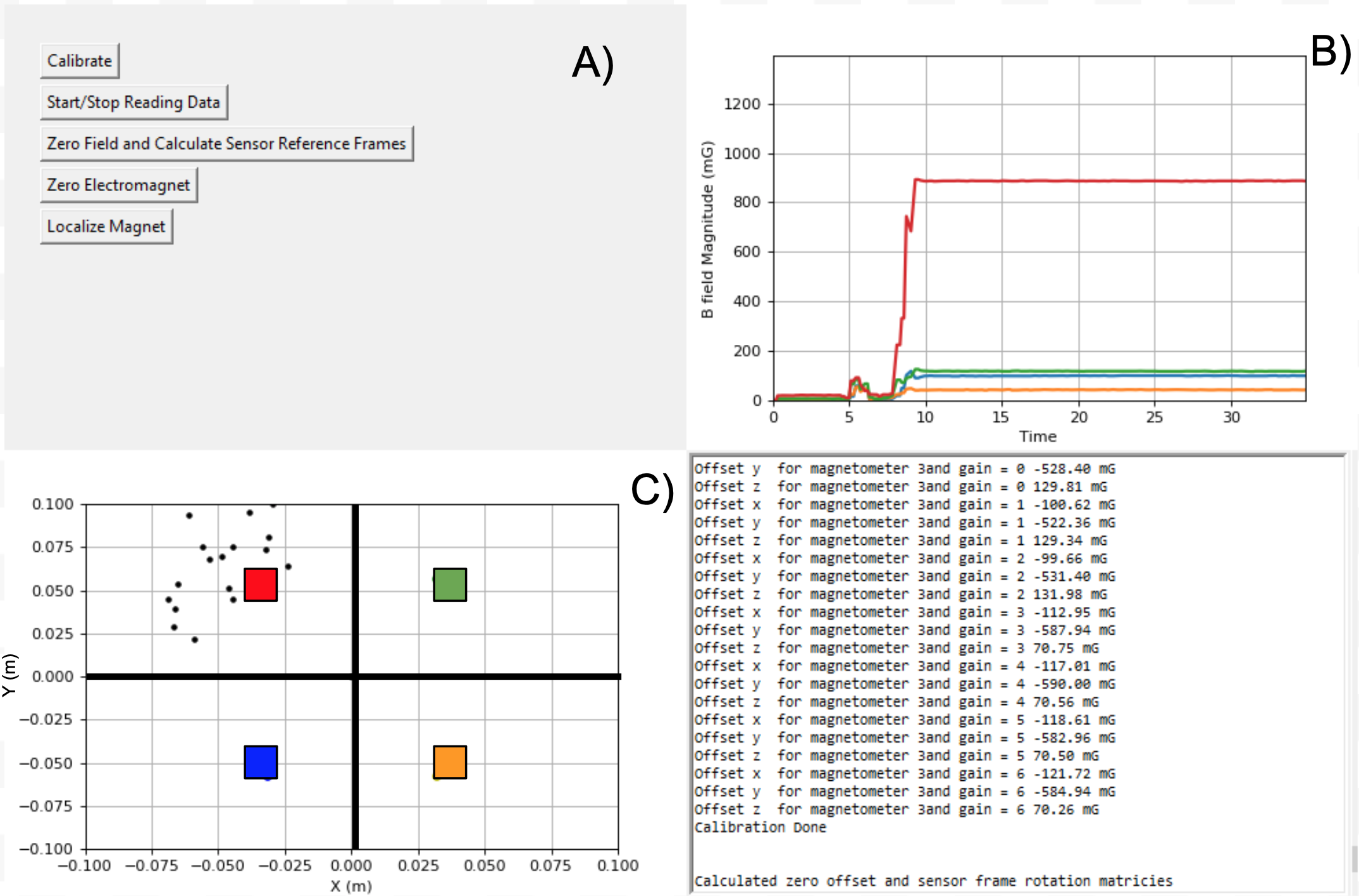
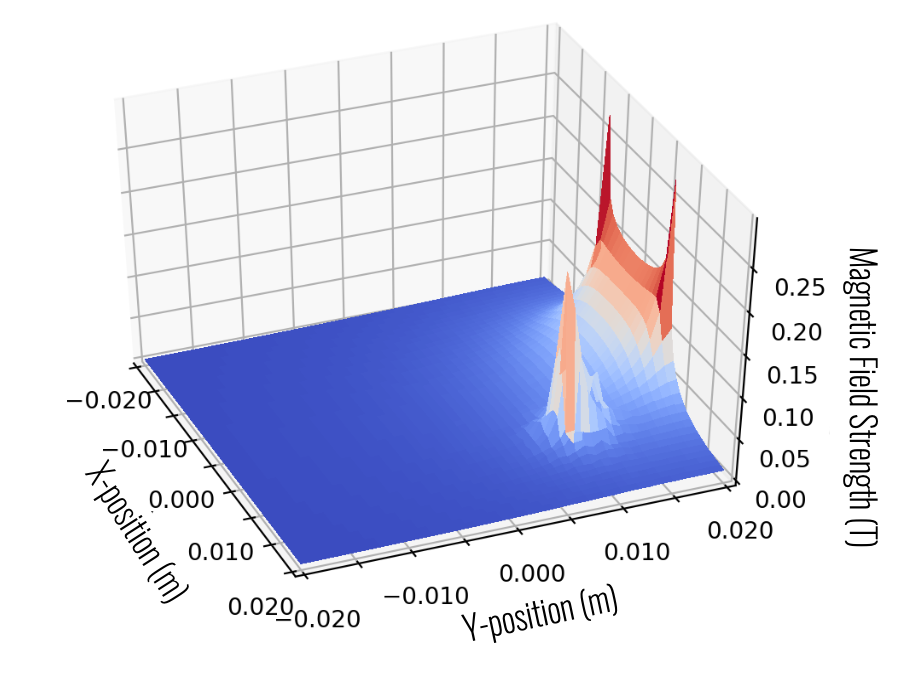
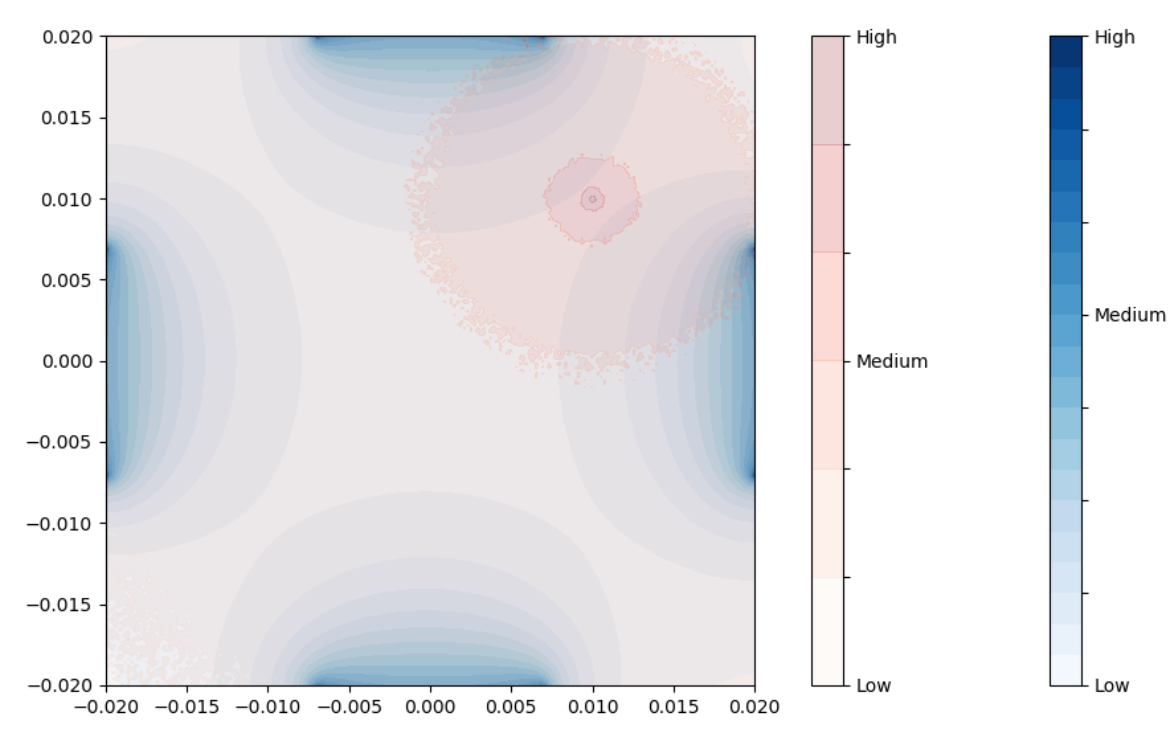
Magnetic drug delivery focuses a cancer drug to a target area by coating a colloidal mixture of ferrofluid nanoparticles and a suspension fluid with therapeutic drugs, injecting the mixture into the body, and delivering it to the target area in vivo by manipulating an external magnetic field. While previous research has explored regarding the efficacy of magnetic drug delivery, little has been done to implement a control system that moves the ferrofluid to a specified location.